我們來看下圖：

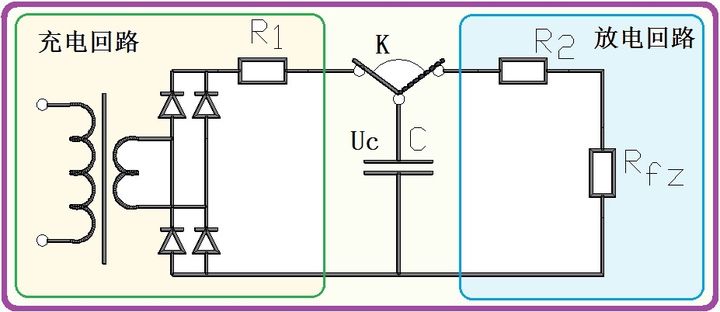
圖中左側(cè)是電容C的充電回路,，圖中右側(cè)是電容C的放電回路,。充電和放電的轉(zhuǎn)換依靠開關(guān)K來實現(xiàn)。圖中的R1是充電線路電阻,，R2是放電的線路電阻,，Rfz是負載電阻。由于題主未談及充電回路,，因此我們把它忽略掉,，僅僅討論放電回路。

我們來設(shè)想一下,，現(xiàn)在電容上的電壓已經(jīng)充滿,，電壓值為Uc。現(xiàn)在我們把開關(guān)K撥到右側(cè),，也即R2的左側(cè),。

我們看如下幾件事：

第一件事：電容與電阻的乘積

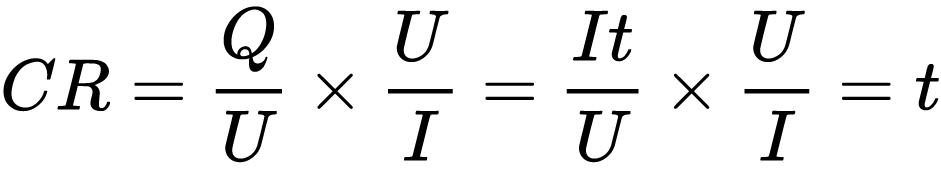
也就是說，電容與電阻的乘積是時間,。

第二件事：放電回路分析

當放電時,，電容相當于電源。根據(jù)基爾霍夫電壓KVL定律,，我們有：

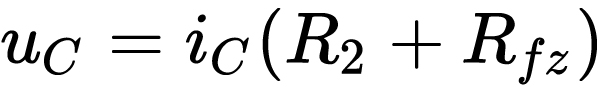
注意,，這里的電容電壓和電容電流均是時間的函數(shù)，電壓[公式]從Uc開始逐漸減小,，而電流[公式]也逐漸減小,。因此電容上的電壓有如下規(guī)律：

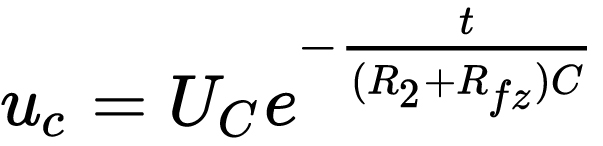
我們令

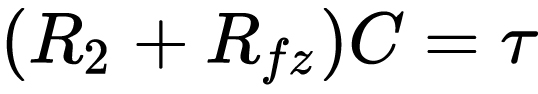
這里的[公式]又被稱為時間常數(shù)，它的值等于放電回路的線路電阻R2與負載電阻Rfz之和,，再乘以電容C得到的積,。我們把這個式子代入到上式中，得到：

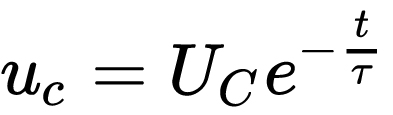
當上式中t=0時,，

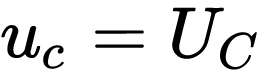
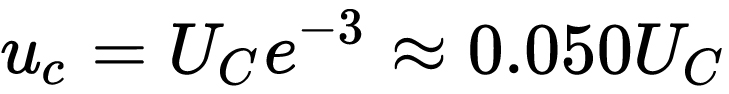當上式中時,，，相當于電容上的電壓已經(jīng)放完了,。

放電曲線如下：

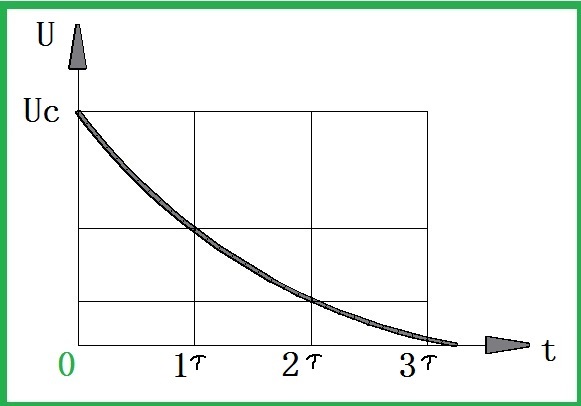
結(jié)論：

答案是：電容放電其實是有時間性的,。在時刻0,，電容上的電壓為Uc，而在3倍時間常數(shù)時,，電容上的電壓只有5%Uc的電壓了,。

可見，電容放電的電壓值是時間的函數(shù),。

同時,，在時刻零，電流最大,。隨著時間的推移,，電流越來越小。當時間等于5倍時間常數(shù)時,，放電電流基本上等于零,。